中国科学技术大学王奉超教授与诺贝尔物理学奖得主、英国曼彻斯特大学安德烈·海姆教授团队合作,在纳米限域毛细凝聚研究方面取得了重要进展:他们建立了纳米限域毛细凝聚的新理论,修正了经典的开尔文方程,并将方程适用性拓展到亚纳米尺度。研究成果刊登在12月10日出版的国际著名学术期刊《自然》上。
什么是毛细凝聚?
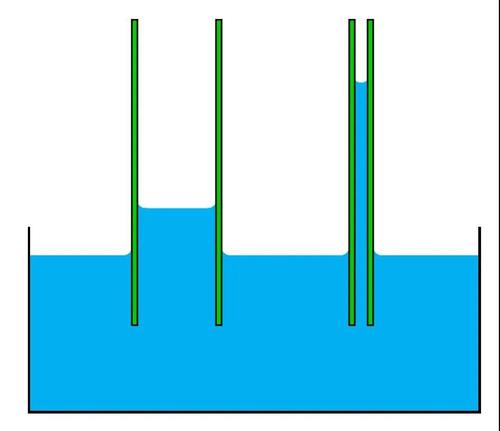
你可能会注意到,水在玻璃杯壁处的液面要比中间略高一些,这是界面处表面张力的作用。水对玻璃是浸润的,也就是说,水和玻璃接触时,接触角为锐角,水更倾向于在玻璃表面铺展开来;相对的,水对荷叶就是不浸润的,雨滴落在荷叶上时,会形成一个一个的小水珠。
对一杯水而言,弯曲界面的范围太小,几乎不会影响到水的性质,可以把水面当成平的来处理;但是当系统变小时,就会有很多有意思的事情发生。比如无处不在的毛细现象:浸润液体会在细管道内自发地向上爬升。钢笔的笔尖利用毛细作用引导墨水。植物能生长也得益于毛细现象:土壤中的孔隙形成了天然的毛细管道,地下水顺着这些管道向上爬,才能被植物的根系所吸收;植物体内的导管也是毛细通道,将水逆着重力向上运输,让水参与植物的光合作用等生命活动。再比如,上面所说的毛细凝聚现象。
在毛细作用下,水在玻璃管内爬升。玻璃管越细,水爬升越高。
水蒸气为什么会凝聚?
我们可以简单认为,空气只能承载一定量的水蒸气,当空气中的水蒸气多到超过一个临界点,多余的那部分会从空气中跑出来,凝聚成水。我们可以用蒸气压表示空气中水含量的多少,水开始凝聚的临界分压强叫做水的饱和蒸气压,我们说的相对湿度,就是当前水蒸气在空气中的分压和饱和蒸气压的比值。
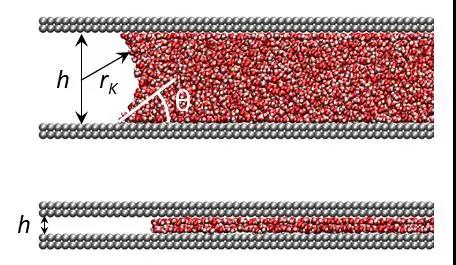
对小的通道,情况又有不同:受表面张力和弯曲界面的影响,水在小通道内会更容易凝聚:在分压没到饱和蒸气压的时候,水就凝聚了,这就是毛细凝聚现象。凝聚压强的变化被科学家威廉·汤姆逊(后来被册封为开尔文勋爵)在150年前定量描述:知道通道的尺寸、液体和固体材料间的接触角,我们就能通过当前的温度、水的表面张力系数等一系列参数算出新的凝聚压强。该理论后来被称为开尔文方程。这是一个描述宏观体系的方程,但是已经被证明可以描述尺寸在10纳米左右(约千分之一人类头发直径)的通道内的凝聚现象。
(上)在通道内定义弯曲液面的接触角θ;(下)当通道只有几层水分子厚时,弯曲液面不存在,接触角无法被定义。
经典开尔文方程受到局限
毛细通道进一步缩小到纳米/亚纳米尺度时,只有几个原子那么大,即“限域系统”。此时,通道内可能只能容纳一两层水分子,“弯曲液面”不存在,没有曲率半径,开尔文方程就不适用了。
如何描述这个尺寸下的毛细凝聚现象呢?带着这样的问题,中科大王奉超教授和2010年诺奖得主Andre Geim教授课题组合作,在用石墨烯搭建的纳米毛细通道里,测量了水的凝聚压强,并通过理论分析,给出了开尔文方程的新形式。
纳米限域毛细凝聚示意图
原子尺度下的物质难于直接观测,如何表征通道内是否发生凝聚呢?科学家想出了一个巧妙的方法:由于通道只有几层石墨烯厚,上下壁面间存在的相互作用——范德华力,使得通道的上壁面在通道内没有水时会向内凹。当凝聚发生时,水“填充”进通道内,把壁面“顶”起来,这样,通道壁面的“变形”就消失了。这个变形可以通过原子力显微镜观测。在一个密闭容器中通入不同湿度的氮气,记录通道壁面的变形情况,就可以测定水的凝聚情况。
水分子(红色)在石墨烯通道(灰色)内发生凝聚后,通道的变形消失。
为了解释实验现象,王奉超教授放弃了原开尔文方程中弯液面的曲率半径、接触角等在微观尺度下无法准确定义的概念,认为石墨烯通道内的毛细凝聚主要是因为固体和液体界面的相互作用。
在传统的针对宏观系统的力学理论体系及下,介质被假定为连续的,即水的密度处处是常数,固液界面能一般也被认为是一个常数。但是在微观尺度下,实验上已经观察到液体的密度在固液交界处呈现明显的分层结构,连续介质假设未必仍然适用。
在微观尺度修正开尔文方程
意识到固液界面的相互作用能会改变后,王奉超教授通过理论推导,将开尔文方程在介观尺度下重写。基于新方程进行的计算机模拟和实验结果吻合良好,表明修正后的开尔文方程可以定量描述毛细凝聚现象。
王奉超教授在实验室
这项研究揭示了固液界面能的尺寸效应,修正了经典的开尔文方程,建立了纳米限域毛细凝聚的新理论,对该极限尺度的最新实验结果及其力学机理进行了合理解释,阐述了固液界面力学作用在纳米/亚纳米尺度的毛细凝聚中扮演的重要角色。这项研究成果论文12月10日发表在 《自然》上。
毛细凝聚现象在微电子、制药、食品和其他诸多行业中都非常重要。这次突破将加深我们对毛细凝聚现象机理的理解,进而可能在多个领域具有非常重要的实际应用前景。
“经典力学理论已经在宏观尺度上对固液体系给出了优美的描述,但在微观尺度上还缺乏普遍适用性;我们希望可以继续研究,对微观世界的固液界面现象也给出合理的解释。”王教授说。
来源:科技日报 (图片由中国科学技术大学提供)